Heap

-

In today’s topic, I will be talking about HEAP. Just like AVL Tree and B-Tree, Heaps is also part of the Binary Search Tree. So what makes heap different? If in AVL Tree, every time we input something they will be sorted in a way that the left child will always have less value than the parent and the right child will have greater value than the parent and each node will be assigned to a height, in Heap the data will be inserted based on their arrival from the most left whether it satisfies the Binary Search Tree rules or not but we have to keep in mind that the parent node should be greater or equal to the key value of the child node for when it’s Max-Heap and less or equal to the key value of the child node for when it’s Min-Heap and each node will be assigned to a key based on their place on the tree. 

To understand more about the difference, here’s an example of insertion for AVL Tree and Max-Heap.

Say that the inserted data queue are, 35, 33, 42, 10, 14, 19, 27, 44, 26, and 31.

For AVL Tree, it would look like this, 


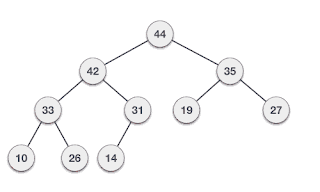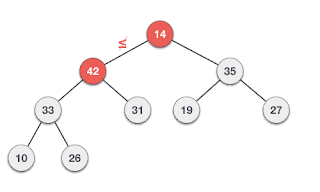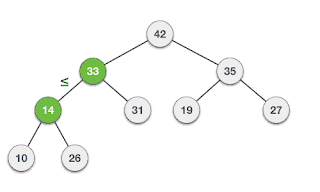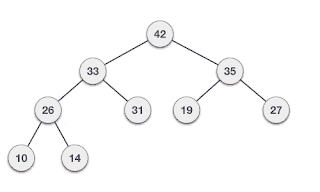
And for Heap, it would look like this, 


We can see that on the Heap Tree number 33 is on the left and number 31 is on the right, which doesn’t satisfy Binary Search Tree rules. But, we can see that the value of every parent is always greater than the children.

So basically, Heap just guarantees that elements on higher levels are greater (for Max-Heap) or smaller (for Min-Heap) than elements on lower levels, whereas AVL Tree guarantees order (from "left" to "right"). Both trees guarantee a balanced tree wherein AVL Tree it’s guaranteed by counting the balance factor, in Heap, it’s guaranteed by always inserting from left to right which made a complete binary tree.

A heap is a partially ordered binary tree where a binary tree is mapped onto an array so that the node in position i is the parent of the nodes in positions 2*i and (2*i + 1) if of course, they exist. Heaps are great for implementing a priority queue because of the largest and smallest element at the root of the tree for a max-heap and a min-heap respectively. We use a max-heap for a max-priority queue and a min-heap for a min-priority queue.

 In Heap, to sort it we use heapify up or down, for heapify up, it sorts the data in reverse by repeatedly placing the largest unsorted element into its correct place. It does so by repeatedly (1) removing the maximum value in the heap (the value in the root node), (2) putting that value into the sorted array, and (3) rebuilding the heap with one fewer elements, vice versa for heapify down. Note that heapsort does not need two separate arrays, it can use the same array for the heap and the sorted array.  

Insertion

Max-Heap
1.      Create a new node at the end of heap.
2.      Assign a new value to the node.
3.      Compare the value of this child node with its parent.
4.      If the value of the parent is greater than the child, then swap them.
5.      Repeat steps 3 & 4 until Heap property holds.

Min-Heap
1.      Create a new node at the end of heap.
2.      Assign a new value to the node.
3.      Compare the value of this child node with its parent.
4.      If the value of the parent is less than the child, then swap them.
5.      Repeat steps 3 & 4 until Heap property holds.

Deletion 


Deletion in Max (or Min) Heap always happens at the root to remove the Maximum (or minimum) value.

Max-Heap
1.      Remove root node.
2.      Move the last element of the last level to root.
3.      Compare the value of this child node with its parent.
4.      If the value of the parent is less than the child, then swap them.
5.      Repeat steps 3 & 4 until Heap property holds.

Min-Heap
1.      Remove root node.
2.      Move the last element of the last level to root.
3.      Compare the value of this child node with its parent.
4.      If the value of the parent is less than the child, then swap them.
5.      Repeat steps 3 & 4 until Heap property holds.

Sources : 

https://www.codesdope.com/blog/article/priority-queue-using-heap/
https://www.sparknotes.com/cs/sorting/heap/summary/ 
https://www.tutorialspoint.com/data_structures_algorithms/heap_data_structure.htm
https://visualgo.net/en/avl
https://visualgo.net/en/heap



Comments

Post a Comment

Popular posts from this blog

Even Semester Full Summary

-
Image
Nama: Aisyah Amalia NIM: 2301904370 Kelas: CB01-CL Hari: June 10th, 2020 Lecturer: Ferdinand Ariandy Luwinda (D4522), Henry Chong (D4460) First Part of Even Semester For the first meeting, I've learned about LINKED LIST. So what is linked list? Linked list is a dynamic data structure, where each element is a separate object. If in array we can easily access the elements in it by the index--because it stores the value in a consecutive memory location, in linked list we can’t do that because in linked list it uses random memory location. Now if you think “Then, isn't array better than?” well in array you can’t easily do insertions and deletions, but in linked list you can easily do push(for insertion) or pop(for deletion). Other than that, if in array you have to give a fixed memory to use in your program, in linked list the number of nodes is not fixed and can grow or shrink on demand, hence it’s called a dynamic data structure. This feature is very use...
Read more

Linked List and Stack and Queue

-
Image
LINKED LIST For the first meeting, I've learned about LINKED LIST. So what is linked list? Linked list is a dynamic data structure, where each element is a separate object. If in array we can easily access the elements in it by the index--because it stores the value in a consecutive memory location, in linked list we can’t do that because in linked list it uses random memory location. Now if you think “Then, isn't array better than?” well in array you can’t easily do insertions and deletions, but in linked list you can easily do push(for insertion) or pop(for deletion). Other than that, if in array you have to give a fixed memory to use in your program, in linked list the number of nodes is not fixed and can grow or shrink on demand, hence it’s called a dynamic data structure. This feature is very useful when you have to deal with an unknown number of objects. One of the disadvantage of linked list is that it uses more memory compares with an array, it adds an extra 4 b...
Read more

First Part of Even Semester

-
Image
For the first meeting, I've learned about LINKED LIST. So what is linked list? Linked list is a dynamic data structure, where each element is a separate object. If in array we can easily access the elements in it by the index--because it stores the value in a consecutive memory location, in linked list we can’t do that because in linked list it uses random memory location. Now if you think “Then, isn't array better than?” well in array you can’t easily do insertions and deletions, but in linked list you can easily do push(for insertion) or pop(for deletion). Other than that, if in array you have to give a fixed memory to use in your program, in linked list the number of nodes is not fixed and can grow or shrink on demand, hence it’s called a dynamic data structure. This feature is very useful when you have to deal with an unknown number of objects. One of the disadvantage of linked list is that it uses more memory compares with an array, it adds an extra 4 bytes (on 3...
Read more